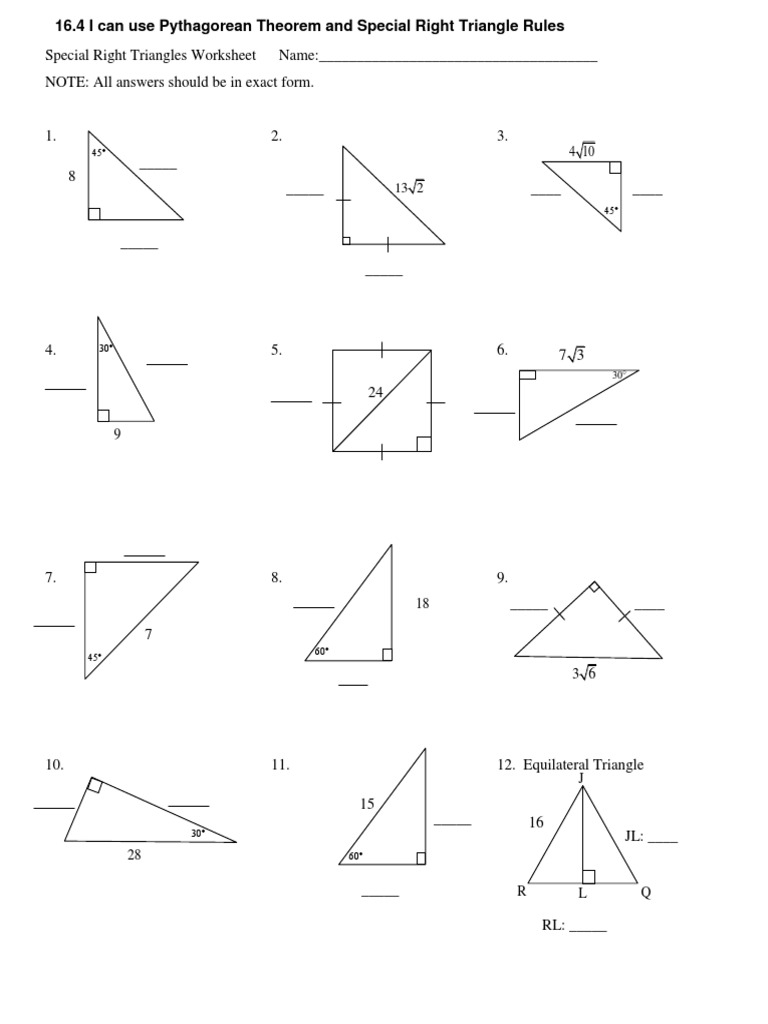
Special right triangles are a unique type of triangle that have angles which are always in a specific ratio. These triangles have angles of 30, 60, and 90 degrees or 45, 45, and 90 degrees. They have special properties that make them useful in trigonometry and geometry.
When working with special right triangles, it is important to understand the relationships between the sides and angles. By using trigonometric functions such as sine, cosine, and tangent, students can solve for missing sides or angles in these triangles. This worksheet is designed to help students practice applying these concepts to special right triangles.
 Special Right Triangles PDF Triangle Length Worksheets Library (worksheets.clipart-library.com)
Special Right Triangles PDF Triangle Length Worksheets Library (worksheets.clipart-library.com)
One common type of special right triangle is the 30-60-90 triangle. In this triangle, the angles are 30, 60, and 90 degrees. The sides are always in the ratio of 1:√3:2. Students can use this ratio to find the lengths of the sides when given one side length. They can also use trigonometric functions to solve for missing angles or sides.
Another type of special right triangle is the 45-45-90 triangle. In this triangle, the angles are 45, 45, and 90 degrees. The sides are always in the ratio of 1:1:√2. Students can use this ratio to find the lengths of the sides when given one side length. They can also use trigonometric functions to solve for missing angles or sides.
This worksheet provides students with a variety of problems involving special right triangles. They will need to apply their knowledge of trigonometry and the properties of special right triangles to solve for missing sides or angles. By practicing with this worksheet, students can improve their skills and gain a better understanding of these unique triangles.
Overall, the Special Right Triangles Worksheet is a valuable tool for students to practice applying trigonometric functions and properties of special right triangles. By working through the problems on this worksheet, students can improve their problem-solving skills and deepen their understanding of these important geometric concepts.
